Приложение для курсовой «Экосистема кроликов и лис»
Всего продано 1
Возвратов 0
Хороших отзывов 0
Плохих отзывов 0
В АРХИВЕ ПРЕДСТАВЛЕНА ТОЛЬКО ПРОГРАММА С НЕКОТОРЫМИ ТЕОРЕТИЧЕСКИМИ СВЕДЕНИЯМИ. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА ОТСУТСТВУЕТ!
Вариант 2.7
Рассмотрим простую экосистему, состоящую из кроликов, для которых имеется неограниченный запас пищи, и лис, которые для пропитания охотятся за кроликами. Классическая математическая модель, принадлежащая Вольтерра, описывает эту систему двумя нелинейными уравнениями первого порядка:
dr/dt = 2r -αrf, r (0) = r0,
df/dt=-f + αrf, f(0) = f0.
Здесь t-время, r = r (t) - число кроликов, f = f(t)- число лис и α - поло¬жительная константа. При α = 0 две популяции не взаимодействуют, и кролики делают то, что у кроликов получается лучше всего, а лисы вымирают от голода. При α > 0 лисы встречают кроликов с вероятностью, пропорциональной произведению числа тех и других. В результате таких встреч число кроликов убывает, а число лис (по менее очевидным причинам) возрастает.
Исследуйте поведение этой системы для α = 0.01 и различных значений r0 и f0, простирающихся от 2 или 3 до нескольких тысяч. Нарисуйте графики наиболее интересных решений. Начертите также график с осями r и f. Поскольку мы умалчиваем о единицах измерения, нет причин ограничивать r и f только целыми значениями.
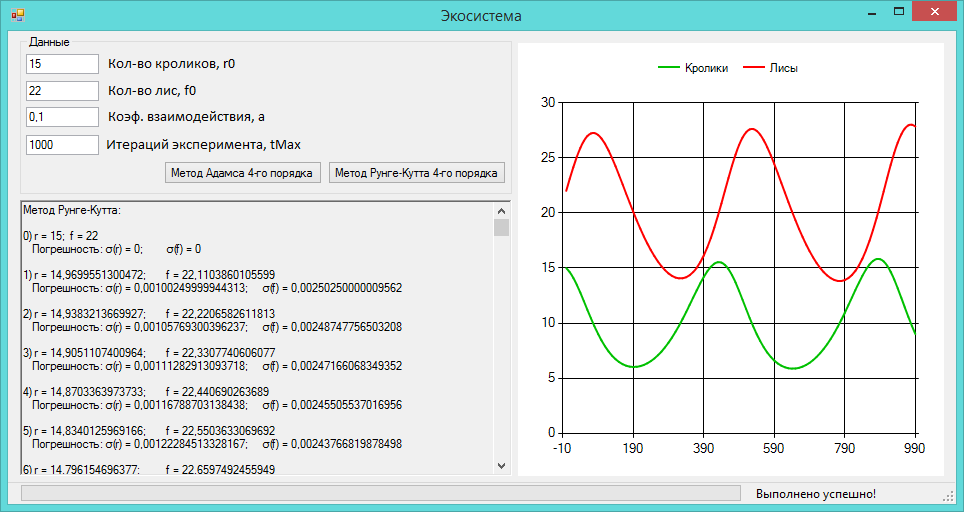
(а) Вычислите решение для r0 = 300 и f0 = 150. Вы должны обнаружить, что поведение системы периодично с периодом, очень близким к 5 единицам времени. Иными словами, r(0) ≈ r(5) и f (0) ≈ f(5).
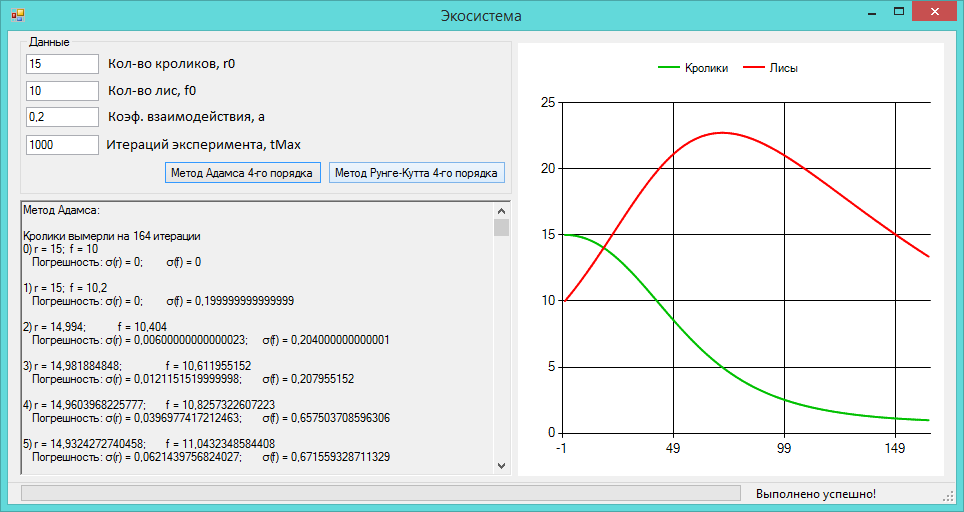
(б) Вычислите решение для r0 = 15 и f0 = 22. Вы должны получить, что число кроликов в конечном счете становится меньше 1. Это можно интерпретировать так, что кролики вымирают. Найдите начальные условия, которые обрекают на вымирание лис. Найдите начальные условия с r0 = f0, при которых вымирают оба вида.
(в) Может ли какая-либо компонента точного решения стать отрицательной? Может ли стать отрицательным численное решение? Что произойдет в этом случае? (На практике ответы на последние два вопроса могут зависеть от заданных вами границ погрешностей.)
(г) Было предложено много модификаций этой простой модели, чтобы более полно отразить то, что происходит в природе. Например, можно воспрепятствовать неограниченному возрастанию числа кроликов, заменив первое уравнение на
dr/dt=2(1-r/R)r-αrf
Теперь даже при α = 0 число кроликов никогда не может превысить R. Выберите какое-либо разумное значение для R и вновь рассмотрите некоторые из поставленных вопросов. В частности, что произойдет с периодичностью решений?
Вариант 2.7
Рассмотрим простую экосистему, состоящую из кроликов, для которых имеется неограниченный запас пищи, и лис, которые для пропитания охотятся за кроликами. Классическая математическая модель, принадлежащая Вольтерра, описывает эту систему двумя нелинейными уравнениями первого порядка:
dr/dt = 2r -αrf, r (0) = r0,
df/dt=-f + αrf, f(0) = f0.
Здесь t-время, r = r (t) - число кроликов, f = f(t)- число лис и α - поло¬жительная константа. При α = 0 две популяции не взаимодействуют, и кролики делают то, что у кроликов получается лучше всего, а лисы вымирают от голода. При α > 0 лисы встречают кроликов с вероятностью, пропорциональной произведению числа тех и других. В результате таких встреч число кроликов убывает, а число лис (по менее очевидным причинам) возрастает.
Исследуйте поведение этой системы для α = 0.01 и различных значений r0 и f0, простирающихся от 2 или 3 до нескольких тысяч. Нарисуйте графики наиболее интересных решений. Начертите также график с осями r и f. Поскольку мы умалчиваем о единицах измерения, нет причин ограничивать r и f только целыми значениями.
(а) Вычислите решение для r0 = 300 и f0 = 150. Вы должны обнаружить, что поведение системы периодично с периодом, очень близким к 5 единицам времени. Иными словами, r(0) ≈ r(5) и f (0) ≈ f(5).
(б) Вычислите решение для r0 = 15 и f0 = 22. Вы должны получить, что число кроликов в конечном счете становится меньше 1. Это можно интерпретировать так, что кролики вымирают. Найдите начальные условия, которые обрекают на вымирание лис. Найдите начальные условия с r0 = f0, при которых вымирают оба вида.
(в) Может ли какая-либо компонента точного решения стать отрицательной? Может ли стать отрицательным численное решение? Что произойдет в этом случае? (На практике ответы на последние два вопроса могут зависеть от заданных вами границ погрешностей.)
(г) Было предложено много модификаций этой простой модели, чтобы более полно отразить то, что происходит в природе. Например, можно воспрепятствовать неограниченному возрастанию числа кроликов, заменив первое уравнение на
dr/dt=2(1-r/R)r-αrf
Теперь даже при α = 0 число кроликов никогда не может превысить R. Выберите какое-либо разумное значение для R и вновь рассмотрите некоторые из поставленных вопросов. В частности, что произойдет с периодичностью решений?